The goal of bws is to provide a user-friendly and efficient implementation of the Bayesian Weighted Sums (BWS) described by Hamra, Maclehose, Croen, Kauffman, and Newschaffer (2021) with some extensions to work with binary and count response data.
You can install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("phuchonguyen/bws")This is a basic example which shows you how to fit BWS:
## We first need to simulate some data
set.seed(123)
N <- 100
P <- 3
K <- 2
X <- matrix(rnorm(N*P), N, P)
Z <- matrix(rnorm(N*K), N, K) # confounders
w <- c(0.3, 0.2, 0.5)
theta0 <- 2
theta1 <- 3
beta <- runif(K, 0.5, 1.5)
y <- theta0 + theta1*theta1*(X%*%w) + Z%*%beta + rnorm(N)
## Fitting BWS is simple
fit <- bws::bws(iter = 2000, y = y, X = X, Z = Z,
# additional arguments for rstan::sampling
chains = 4, cores = 2, show_messages = FALSE)
#> Warning: replacing previous import 'lifecycle::last_warnings' by
#> 'rlang::last_warnings' when loading 'tibble'
#> Warning: replacing previous import 'lifecycle::last_warnings' by
#> 'rlang::last_warnings' when loading 'pillar'Since the implementation uses Stan and returns an
rstanfit object, users can enjoy all the functionalities
provided in rstan to analyze the fitted model:
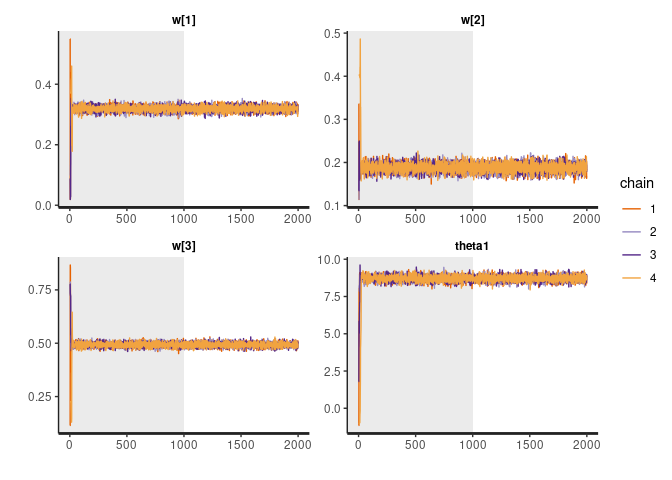
rstan::traceplot(fit, pars = c("w", "theta1"), inc_warmup = TRUE, nrow = 2)
print(fit, pars = c("w", "theta1"))
#> Inference for Stan model: bws.
#> 4 chains, each with iter=2000; warmup=1000; thin=1;
#> post-warmup draws per chain=1000, total post-warmup draws=4000.
#>
#> mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
#> w[1] 0.32 0 0.01 0.30 0.31 0.32 0.33 0.34 5292 1
#> w[2] 0.19 0 0.01 0.17 0.18 0.19 0.19 0.21 5750 1
#> w[3] 0.49 0 0.01 0.47 0.49 0.49 0.50 0.51 6125 1
#> theta1 8.71 0 0.19 8.34 8.59 8.71 8.84 9.08 5388 1
#>
#> Samples were drawn using NUTS(diag_e) at Mon Jun 13 00:06:38 2022.
#> For each parameter, n_eff is a crude measure of effective sample size,
#> and Rhat is the potential scale reduction factor on split chains (at
#> convergence, Rhat=1).
rstan::plot(fit)
#> ci_level: 0.8 (80% intervals)
#> outer_level: 0.95 (95% intervals)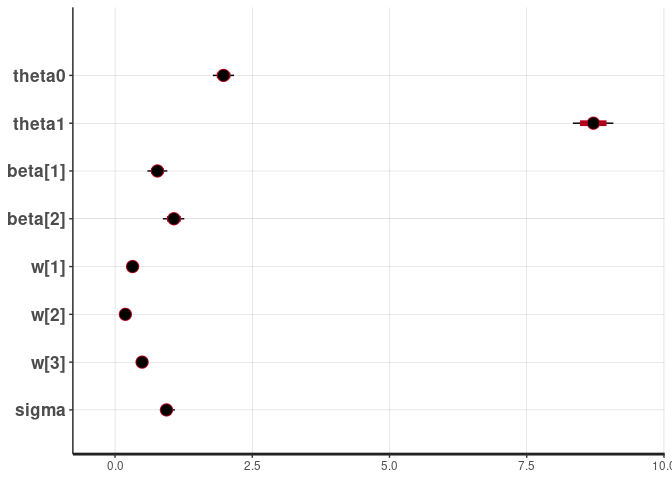
The model inferred the correct weights, which are set to 0.3, 0.2, 0.5 in the simulation.
Hamra, G.B.; Maclehose, R.F.; Croen, L.; Kauffman, E.M.; Newschaffer, C. Bayesian Weighted Sums: A Flexible Approach to Estimate Summed Mixture Effects. International Journal of Environmental Research and Public Health 2021, 18, 1373. link