

extrememix implements Bayesian estimation of extreme
value mixture models, estimating the threshold over which a Generalized
Pareto distribution can be assumed as well as high quantiles and other
measures of interest in extreme value theory.
The package extrememix can be installed from GitHub
using the command
# install.packages("devtools")
#devtools::install_github("manueleleonelli/extrememix")and loaded in R with
library(extrememix)
library(ggplot2)We consider the rainfall dataset reporting the monthly
maxima daily rainfall (in mm) recorded at the Retiro station in the city
of Madrid between 1985 and 2020. The data consists of 414 monthly maxima
since 18 months were discarded in which no rain was observed.
data("rainfall")
ggplot(data = data.frame(rainfall), aes(x=rainfall)) +
geom_histogram(binwidth = 2*length(rainfall)^(-1/3)*IQR(rainfall), colour="black", fill="white") + theme_bw()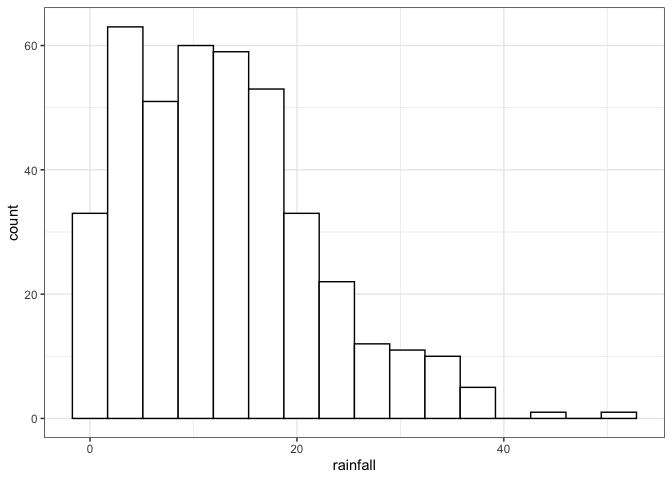
The data histogram shows that the maximum rainfall observed in a day is around 50mm. Although there are some extreme observations, the distribution appears to be right-bounded.
We start our analysis fitting the GGPD model (gamma bulk/GPD tail)
using the function fggpd. We specify the number of
iterations, the burn-in and the thinning via the options
it, burn and thin, respectively.
The prior distribution, the starting values and the variances of the
proposal distributions are automatically chosen, but these can be set by
the user (see below).
rainfall_ggpd <- fggpd(rainfall, it = 50000, burn = 10000, thin = 40)
rainfall_ggpdThe print method for the object model1
gives us an overview of the estimation process, stating the model
fitted, its log-likelihood, the posterior estimate of the shape
parameter \(\xi\) of the GPD and the
probability that the distribution is right-unbounded. Additional details
can be gathered using the summary function.
summary(rainfall_ggpd)
#> estimate lower_ci upper_ci
#> xi -0.14 -0.27 0.05
#> sigma 8.83 6.86 11.80
#> u 13.97 9.05 14.88
#> mu 16.33 14.35 20.40
#> eta 1.16 0.96 1.36The summary reports the posterior estimates as well as
95% posterior credibility intervals of the models’ parameters. The
threshold is estimated at 12.88 and the GPD is therefore estimated over
a proportion of the data equal to 0.4541063.
extrememix includes the function
check_convergence which reports the traceplot and the
auto-correlation plot for the estimated 0.99 quantile. It can be used as
a quick check to ensure convergence of the estimation algorithm. Other R
packages can be used for more in-depth analyses. According to the
output, the estimation of the quantile is stable and therefore it is
likely that the chain reached convergence.
check_convergence(rainfall_ggpd)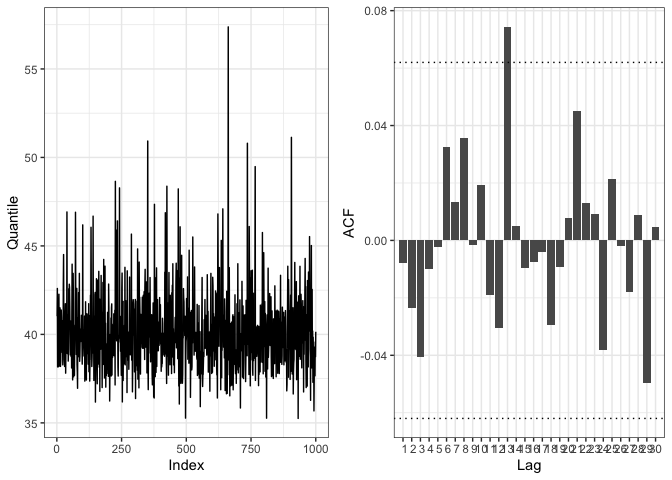
As an alternative model we consider the MGPD (mixture of gammas
bulk/GPD tail) with 2 mixture components. It can be fitted using the
function fmgpd, which needs as input also the number of
components k. In this case we fully specify the model and
the estimation procedure by also giving the starting values, the
variances and the prior distribution.
The starting values can be set creating a list with entries
xi, sigma, u, mu,
eta and w. The proposal variances can be set
creating a list with entries xi, sigma,
u, mu and w (for each mixture
component the parameters \(\mu\) and
\(\eta\) are sampled jointly). The
prior distribution can be set creating a list with entries
u (a vector with the mean and standard deviation of the
prior normal distribution for \(u\)),
mu_mu (a vector with the prior means of the Gamma
distributions for \(\mu\)),
mu_eta (a vector with the prior shapes of the Gamma
distributions for \(\mu\)),
eta_mu (a vector with the prior means of the Gamma
distributions for \(\eta\)) and
eta_eta (a vector with the prior shapes of the Gamma
distributions for \(\eta\)).
start <- list(xi = 0.2, sigma = 5, u = quantile(rainfall,0.9),
mu = c(4,10), eta = c(1,4), w = c(0.5,0.5))
var <- list(xi = 0.001, sigma = 1, u = 2, mu = c(0.1,0.1), w = 0.1)
prior <- list(u = c(22,5), mu_mu = c(4,16), mu_eta = c(0.001,0.001),
eta_mu = c(1,4), eta_eta = c(0.001,0.001))
rainfall_mgpd <- fmgpd(rainfall, k =2, it = 50000, burn = 10000, thin = 40,
start = start, var = var, prior = prior)The summary below shows that an MGPD model is not actually required since the estimate of the weight of one of the two components is zero.
rainfall_mgpd
#> EVMM with 2 Mixtures of Gamma bulk. LogLik -1441.789
#> xi estimated as -0.1348735
#> Probability of unbounded distribution 0.05894106
summary(rainfall_mgpd)
#> estimate lower_ci upper_ci
#> xi -0.13 -0.26 0.04
#> sigma 8.70 6.82 11.96
#> u 13.97 9.10 14.95
#> mu1 0.00 0.00 0.00
#> mu2 16.30 14.19 18.87
#> eta1 0.00 0.00 0.00
#> eta2 1.16 0.98 1.34
#> w1 0.00 0.00 0.00
#> w2 1.00 1.00 1.00Let’s anyway check the convergence of the algorithm to ensure the estimation process went ok.
check_convergence(rainfall_mgpd)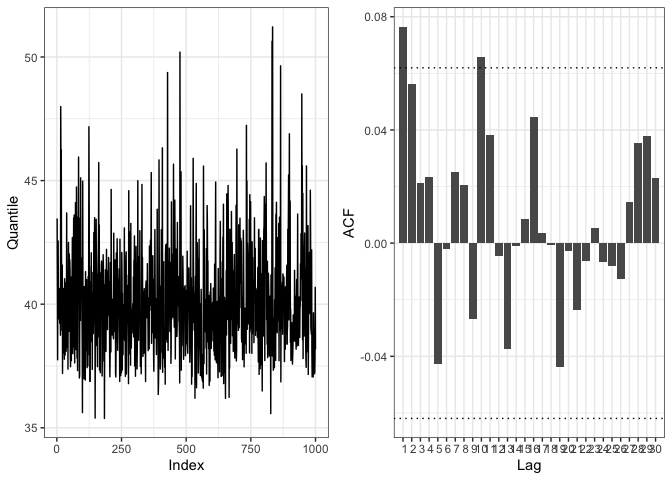
Since the MGPD model has one weight equal to zero, a GGPD is
recommended. We can anyway check that this is the case using model
selection criteria. extrememix implements the AIC, AICc,
BIC, DIC and WAIC criteria in the equally-named functions.
rbind(c(BIC(rainfall_ggpd),BIC(rainfall_mgpd)),c(DIC(rainfall_ggpd),DIC(rainfall_mgpd)),c(WAIC(rainfall_ggpd),WAIC(rainfall_mgpd)))
#> [,1] [,2]
#> [1,] 2913.918 2931.784
#> [2,] 2891.035 2892.770
#> [3,] 2897.241 2896.992For simplicity, here we considered three model selection criteria. BIC, DIC and WAIC all favor the GGPD. As already noticed in the literature, the use of WAIC is recommended and indeed it selects the GGPD model.
We therefore next investigate the use of the GGPD model to assess
rainfall in the city of Madrid. The plot method gives an
overview of the model reporting the histogram of the distributions of
\(\xi\) and \(\sigma\), a plot of the quantiles and a
plot of the predictive distribution.
plot(rainfall_ggpd)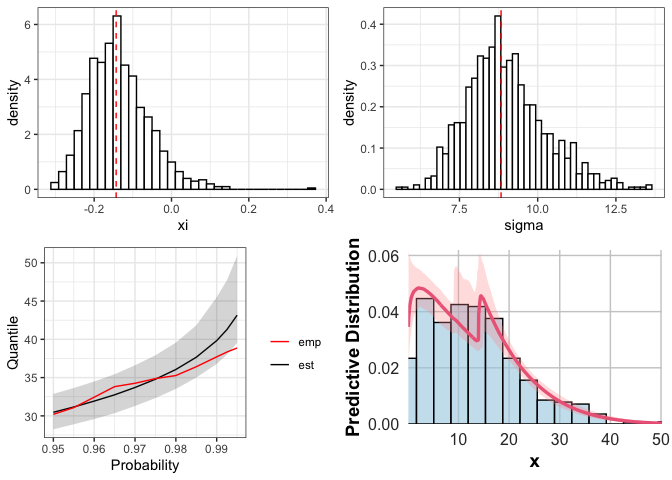
The predictive distribution can be further obtained using the
function pred. The plot shows that the model gives a
faithful description of the tail of the data.
pred(rainfall_ggpd)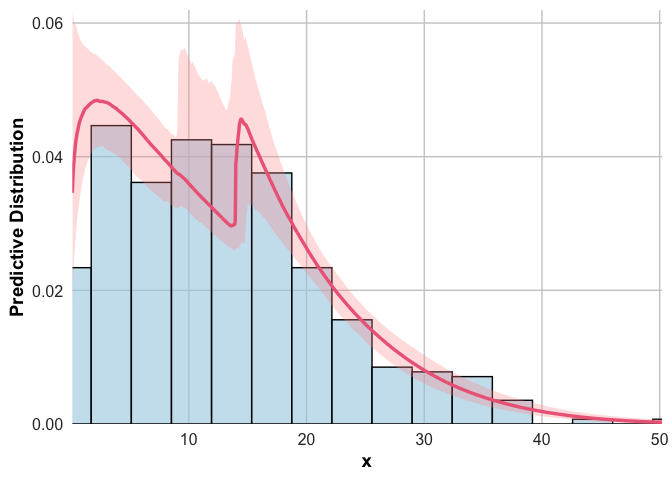
In extreme value analysis there are many measures that are used to
quantify risk: quantiles (implemented in quant), return
levels (in return_level), Value-at-Risk (in
VaR), Expected shortfall (in ES) and Tail VaR
(in TVaR). For instance here we compute the return levels,
i.e. the value that is expected to be equaled or exceeded on average
once every interval of time (T).
return_level(rainfall_ggpd)
#> Level estimate lower_ci upper_ci empirical
#> [1,] 20 30.47 28.24 32.87 30.20
#> [2,] 25 31.93 29.58 34.49 32.44
#> [3,] 30 33.05 30.65 35.84 34.05
#> [4,] 40 34.79 32.33 37.92 34.87
#> [5,] 50 36.06 33.52 39.57 35.27
#> [6,] 60 37.09 34.50 40.88 35.80
#> [7,] 70 37.93 35.23 42.33 36.65
#> [8,] 80 38.64 35.84 43.68 37.02
#> [9,] 90 39.26 36.37 44.65 37.39
#> [10,] 100 39.83 36.79 45.50 37.71
#> [11,] 150 41.79 38.46 48.61 38.52
#> [12,] 200 43.15 39.53 50.89 38.87
#> [13,] 250 44.17 40.35 52.62 41.13
plot(return_level(rainfall_ggpd))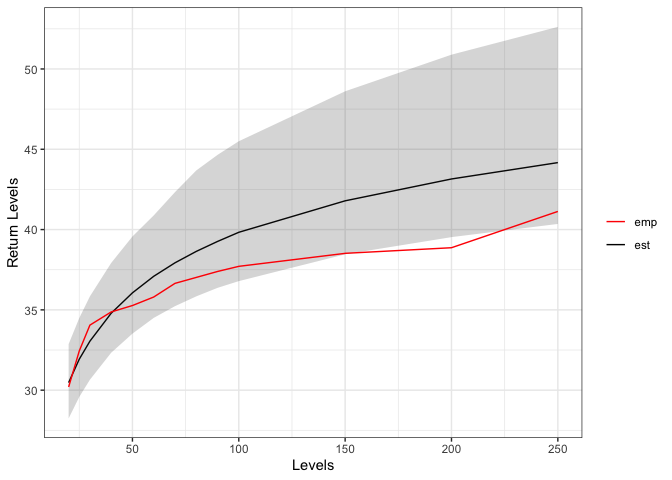
From the output we can see that we expect a rainfall of 30.42 mms to
be equaled or exceeded every 20 months. The width of the credibility
intervals can be chosen with the cred input and the values
at which to compute the return levels can be chosen with
values.
As a different measure, we consider next the expected shortfall, defined as the expected value in the q% of the worst cases. For instance, the code below computes the 1% expected shortfall.
ES(rainfall_ggpd, values = 1)
#> ES_Level estimate lower_ci upper_ci empirical
#> [1,] 1 44.26 40.35 53.45 42.12
plot(ES(rainfall_ggpd, values = 1))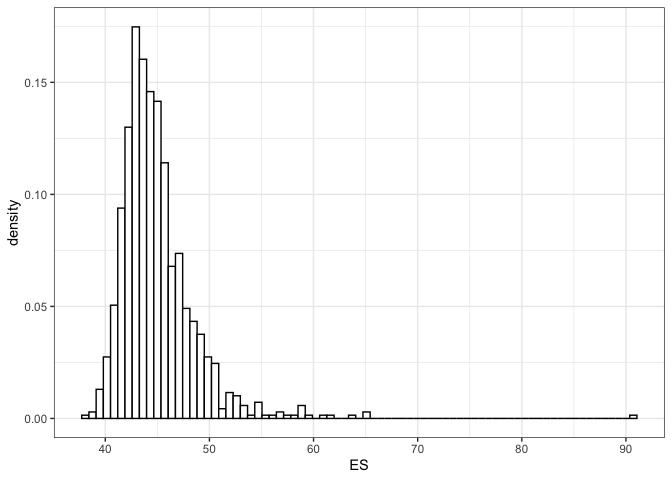 In other words, conditional on observing a value above the 0.99
quantile, the expected rainfall is equal to 44.46mms.
In other words, conditional on observing a value above the 0.99
quantile, the expected rainfall is equal to 44.46mms.
Since we selected a unique values the plotting method
reports the posterior histogram of the estimated quantity.
To conclude the analysis, we can further estimate what is the largest
possible rainfall that could ever be observed in the city of Madrid,
since we observed that \(\xi\) was
often estimated as negative. This can be done with the function
upper_bound.
upper_bound(rainfall_ggpd)
#> Probability of unbounded distribution: 0.052
#> Estimated upper bound at 74.07 with probability 0.948
#> Credibility interval at 0.95 %: ( 53.79 , 321.48 )
plot(upper_bound(rainfall_ggpd), xlim = c(20,400))
#> Upper Bound, with probability 0.948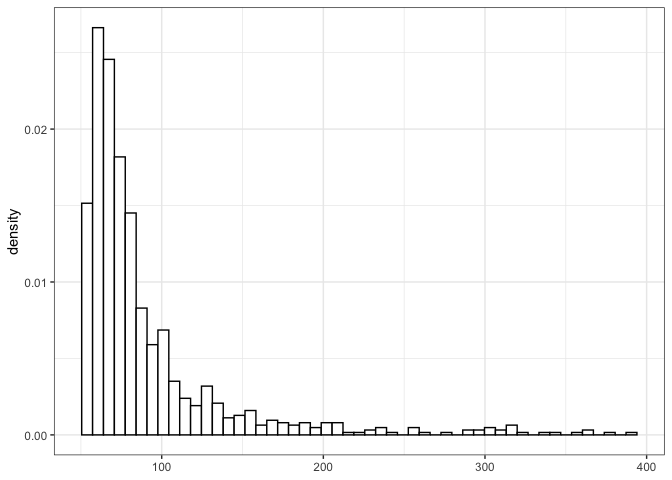
The maximum rainfall that could be observed in Madrid is estimated as
74.07. Furthermore, since in the posterior sample there are some values
of \(\xi\) which are positive, we have
a non-zero probability that the distribution is right-unbounded. The
limits of the histogram are set with the input xlim.